气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t(单位:℃) |
t≤22 |
22<t≤28 |
28<t≤32 |
t>32 |
| 天数 |
6 |
12 |
Y |
Z |
由于工作疏忽,统计表被墨水污染,Y和Z数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
某水果商根据多年的销售经验,六月份的日最高气温t(单位:℃)对西瓜的销售影响如下表:
| 日最高气温t(单位:℃) |
t≤22 |
22<t≤28 |
28<t≤32 |
t>32 |
| 日销售额X(单位:千元) |
2 |
5 |
6 |
8 |
(1)求Y,Z的值;
(2)若视频率为概率,求六月份西瓜日销售额的期望和方差;
(3)在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
已知函数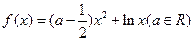 。
。
(I)当a=1时,求 在区间[1,e]的最大值和最小值;
在区间[1,e]的最大值和最小值;
(II)若在区间 上,函数
上,函数 的图象总在直线
的图象总在直线 的下方,求a的取值范围。
的下方,求a的取值范围。
设函数 (1)当
(1)当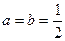 时,求
时,求 的最大值;(2)令
的最大值;(2)令 ,(0
,(0 ≤3),其图象上任意一点
≤3),其图象上任意一点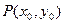 处切线的斜率
处切线的斜率 ≤
≤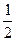 恒成立,求实数
恒成立,求实数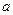 的取值范围;(3)当
的取值范围;(3)当 ,
, ,方程
,方程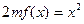 有唯一实数解,求正数
有唯一实数解,求正数 的值。
的值。
已知平面 上的动点
上的动点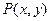 及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是
及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是 ,
, ,且
,且 ·
·
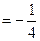 。(1)求动点P的轨迹C的方程;
。(1)求动点P的轨迹C的方程;
(2)已知直线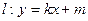 与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足
与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足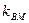 ·
·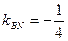 ,求证:直线
,求证:直线 过原点。
过原点。
已知,等差数列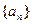 的首项
的首项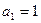 ,公差
,公差 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列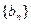 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列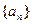
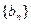 的通项公式;(2)设数列
的通项公式;(2)设数列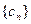 对任意正整数
对任意正整数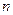 均有
均有 成立,求数列
成立,求数列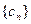 的前
的前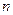 项的和
项的和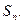
某校积极响应《全面健身条例》,把周五下午5:0 0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
(1)求这两 支球队每月两次都在同一时间活动的频率;
支球队每月两次都在同一时间活动的频率;
(2)设这两支球队每月能同时活动的次数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。