已知N= ,计算N2.
,计算N2.
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若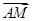 =x
=x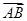 ,
,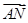 =y
=y ,求
,求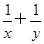 的值.
的值.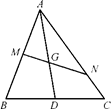
如图,△ABC中,在AC上取一点N,使得AN= AC,在AB上取一点M,使得AM=
AC,在AB上取一点M,使得AM= AB,在BN的延长线上取点P,使得NP=
AB,在BN的延长线上取点P,使得NP=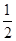 BN,在CM的延长线上取点Q,使得
BN,在CM的延长线上取点Q,使得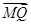 =λ
=λ 时,
时, =
=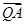 ,试确定λ的值.
,试确定λ的值.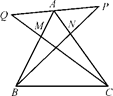
已知点A(2,3),B(5,4),C(7,10),若 =
=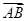 +λ·
+λ·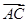 (λ∈R),试问:
(λ∈R),试问:
(1) λ为何值时,点P在第一、三象限角平分线上;
(2) λ为何值时,点P在第三象限.
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD∶DB=BE∶EC=2∶1,AE与CD交于P.设存在λ和μ使 =λ
=λ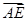 ,
, =μ
=μ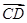 ,
, =a,
=a, =b.
=b.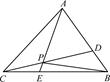
(1) 求λ及μ;
(2) 用a、b表示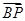 ;
;
(3) 求△PAC的面积.
已知向量a=(6,2),b=(-3,k),若a∥b,求实数k的值.