(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: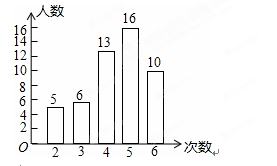
①所调查的七年级50名学生在这个月内做好事次数的平均数是____,众数是_____,极差是 ___
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
(2)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球.
①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?
一水果店是 酒店某种水果的首选供货商,水果店根据该酒店以往每月的需求情况,本月初专门为他们准备了 的这种水果.已知水果店每售出 该水果可获利润10元,未售出的部分每 将亏损6元,以 (单位: , 表示 酒店本月对这种水果的需求量, (元 表示水果店销售这批水果所获得的利润.
(1)求 关于 的函数表达式;
(2)问:当 酒店本月对这种水果的需求量如何时,该水果店销售这批水果所获的利润不少于22000元?
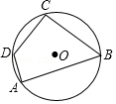
如图,四边形 内接于 , , , , ,求 的长.
某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为 、 、 、 、 五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中, 类二手轿车交易辆数所对应扇形的圆心角为 度.
如图,平行四边形 中, 、 分别是边 、 的中点,求证: .
