我校某同学设计了一个如图所示的“蝴蝶形图案(阴影区域)”来庆祝数学学科节的成功举办.其中 、
、 是过抛物线
是过抛物线 焦点
焦点 的两条弦,且其焦点
的两条弦,且其焦点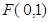 ,
, ,点
,点 为
为 轴上一点,记
轴上一点,记 ,其中
,其中 为锐角.
为锐角.
(1)求抛物线 方程;
方程;
(2)当“蝴蝶形图案”的面积最小时求 的大小.
的大小.
(本小题满分12分)为了提高我市的教育教学水平,市教育局打算从红塔区某学校推荐的10名教师中任选3人去参加支教活动。这10名教师中,语文教师3人,数学教师4人,英语教师3人.
求:(1)选出的语文教师人数多于数学教师人数的概率;
(2)选出的3人中,语文教师人数 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图所示,直三棱柱 的各条棱长均为
的各条棱长均为 ,
,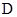 是侧棱
是侧棱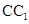 的中点.
的中点.
(1)求证:平面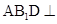 平面
平面 ;
;
(2)求平面 与平面
与平面 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.
(本小题满分12分)设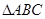 的内角
的内角 所对的边为
所对的边为 ,
,
(1)求角 的大小;
的大小;
(2)若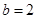 ,
,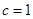 ,
,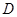 为
为 的中点,求
的中点,求 的长.
的长.
(本小题满分12分)已知函数 (
( 为常数,
为常数, 为自然对数的底数)是实数集
为自然对数的底数)是实数集 上的奇函数,函数
上的奇函数,函数 在区间
在区间 上是减函数.
上是减函数.
(1)求实数 的值;
的值;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数.
的根的个数.
(本小题满分12分)已知等比数列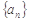 是递增数列,
是递增数列,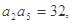
 ,又数列
,又数列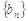 满足
满足 ,
,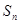 是数列
是数列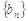 的前
的前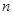 项和.
项和.
(1)求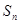 ;
;
(2)若对任意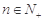 ,都有
,都有 成立,求正整数
成立,求正整数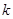 的值
的值