如图所示,抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1-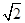 时,切线MA的斜率为-
时,切线MA的斜率为- .
.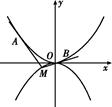
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
已知集合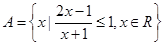 ,集合
,集合 .
.
(1)求集合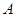 ;
;
(2)若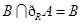 ,求实数
,求实数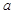 的取值范围.
的取值范围.
如图,已知抛物线 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.
(1)求证:KF平分∠MKN;
(2)O为坐标原点,直线MO、NO分别交准线于点P、Q,求 的最小值.
的最小值.
已知函数 ,
, .若函数
.若函数 依次在
依次在 处取到极值.
处取到极值.
(1)求 的取值范围;
的取值范围;
(2)若 ,求
,求 的值.
的值.
如图,在平面四边形ABCD中,已知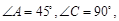
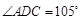 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

(1)求证:DC 平面ABC;
平面ABC;
(2)求直线 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值.
已知数列 的前
的前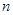 项和为
项和为 ,且
,且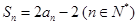 ,数列
,数列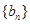 满足
满足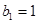 ,且
,且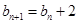 .
.
(Ⅰ)求数列 、
、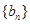 的通项公式;
的通项公式;
(Ⅱ)设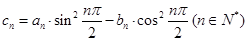 ,求数列
,求数列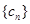 的前
的前 项和
项和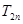 .
.