如图所示,在直角坐标系xOy中,点P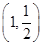 到抛物线C:y2=2px(p>0)的准线的距离为
到抛物线C:y2=2px(p>0)的准线的距离为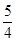 .点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.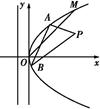
(1)求p,t的值;
(2)求△ABP面积的最大值.
已知数列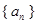 是首项为
是首项为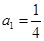 ,公比
,公比 的等比数列. 设
的等比数列. 设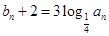
 ,数列
,数列 满足
满足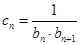 .
.
(Ⅰ)求证:数列 成等差数列;
成等差数列;
(Ⅱ)求数列 的前
的前 项和
项和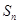 .
.
(考生注意:只能从A,B,C中选择一题作答,并将答案填写在相应字母后的横线上,若多做,则按所做的第一题评阅给分.)
A.选修4-1:几何证明选讲
已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD的值为____.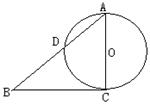
B.选修4-4:坐标系与参数方程
在极坐标系中,已知圆 与直线
与直线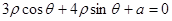 相切,求实数a的值______.
相切,求实数a的值______.
C.选修4-5:不等式选讲
不等式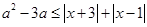 对任意实数
对任意实数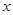 恒成立,求实数
恒成立,求实数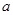 的取值范围____.
的取值范围____.
已知二次函数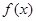 有两个零点
有两个零点 和
和 ,且
,且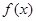 最小值是
最小值是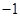 ,函数
,函数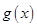 与
与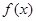 的图象关于原点对称;
的图象关于原点对称;
(1)求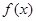 和
和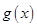 的解析式;
的解析式;
(2)若 在区间
在区间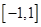 上是增函数,求实数
上是增函数,求实数 的取值范围。
的取值范围。
已知在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,点 的极坐标是
的极坐标是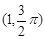 ,曲线C的极坐标方程为
,曲线C的极坐标方程为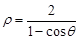 .
.
(I)求点 的直角坐标和曲线C的直角坐标方程;
的直角坐标和曲线C的直角坐标方程;
(II)若经过点 的直线
的直线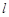 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求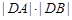 的最小值.
的最小值.
设命题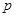 :函数
:函数 是R上的减函数,命题q:
是R上的减函数,命题q: 在
在 上的值域为
上的值域为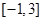 ,若“
,若“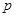 或
或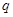 ”为真命题,“
”为真命题,“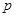 且
且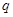 ”为假命题,求实数a的取值范围.
”为假命题,求实数a的取值范围.