已知E(2,2)是抛物线C:y2=2px上一点,经过点(2,0)的直线l与抛物线C交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N.
(1)求抛物线方程及其焦点坐标;
(2)已知O为原点,求证:∠MON为定值.
(本小题满分12分)(解答过程写在试卷上无效)
如图1,一条宽为 的两平行河岸有村庄
的两平行河岸有村庄 和发电站
和发电站 ,村庄
,村庄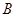 与
与 ,
, 的直线距离都是
的直线距离都是 ,
,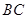 与河岸垂直,垂足为
与河岸垂直,垂足为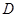 .现要铺设电缆,从发电站
.现要铺设电缆,从发电站 向村庄A,
向村庄A,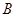 供电.已知铺设地下电缆、水下电缆的费用分别是
供电.已知铺设地下电缆、水下电缆的费用分别是 万元/
万元/ 、4万元/
、4万元/ .
.
(1)如果村庄 与
与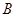 之间原来铺设有旧电缆 (图1中线段
之间原来铺设有旧电缆 (图1中线段 所示),只需对其进行改造即可使用.已知旧电缆的改造费用是
所示),只需对其进行改造即可使用.已知旧电缆的改造费用是 万元/
万元/ .现决定在线段
.现决定在线段 上找得一点
上找得一点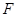 建一配电站,分别向村庄
建一配电站,分别向村庄 ,
,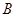 供电,使得在完整利用
供电,使得在完整利用 ,
,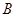 之间旧电缆进行改造的前提下,并要求新铺设的水下电缆长度最短,试求该方案总施工费用的最小值,并确定点
之间旧电缆进行改造的前提下,并要求新铺设的水下电缆长度最短,试求该方案总施工费用的最小值,并确定点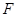 的位置;
的位置;
(2)如图2,点 在线段
在线段 上,且铺设电缆线路为
上,且铺设电缆线路为 ,
, ,
, .若
.若 ,试用
,试用 表示出总施工费用
表示出总施工费用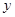 (万元)的解析式,并求
(万元)的解析式,并求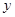 的最小值。
的最小值。
(本小题满分12分)(解答过程写在试卷上无效)
已知函数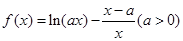
(1)求函数 的最值;
的最值;
(2)当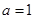 时,是否存在过点
时,是否存在过点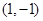 的直线与函数
的直线与函数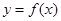 的图像相切?若存在,有多少条?若不存在,说明理由.
的图像相切?若存在,有多少条?若不存在,说明理由.
(本小题满分12分)(解答过程写在试卷上无效)
对于函数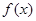 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称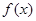 为“局部奇函数”.
为“局部奇函数”. 为定义在
为定义在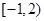 上的“局部奇函数”;
上的“局部奇函数”;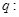 曲线
曲线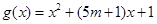 与
与 轴交于不同的两点;
轴交于不同的两点;
若 为假命题,
为假命题,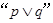 为真命题,求
为真命题,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-5:不等式选讲
已知函数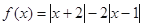
(1)解不等式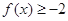 ;
;
(2)对任意 ,都有
,都有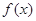
 成立,求实数
成立,求实数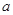 的取值范围.
的取值范围.
(本小题满分14分)已知函数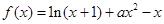 (
(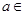 R).
R).
(1)当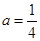 时,求函数
时,求函数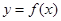 的单调区间;
的单调区间;
(2)若对任意实数 ,当
,当 时,函数
时,函数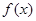 的最大值为
的最大值为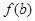 ,求
,求 的取值范围.
的取值范围.