已知抛物线yn＝－(x－an)2＋an(n为正整数，且0＜a1＜a2＜…＜an)与x轴的交点为An－1(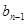
,0)和An(bn,0)．当n＝1时，第1条抛物线y1＝－(x－a1)2＋a1与x轴的交点为A0(0,0)和A1(b1,0)，其他依此类推．
(1) 求a1、b1的值及抛物线y2的解析式；
(2) 抛物线y3的顶点坐标为(____，___)；依此类推第n条抛物线yn的顶点坐标为(_____，_____)(用含n的式子表示)；所有抛物线的顶点坐标满足的函数关系式是_____________；
(3) 探究下列结论：
①若用An－1 An表示第n条抛物线被x轴截得的线段的长，则A0A1=______，An－1 An=____________；
②是否存在经过点A1(b1,0)的直线和所有抛物线都相交，且被每一条抛物线截得的线段的长度都相等？若存在，直接写出直线的表达式；若不存在，请说明理由．
计算：|－4|－(
－1)0+2cos45°+
化简：（
－
)÷
已知：直线
（n为正整数）与两坐标轴围成的三角形面积为
，则
__ ▲ ．
如果一个点能与另外两个点构成直角三角形，则称这个点为另外两个点的勾股点．例如：矩形ABCD中，点C与A，B两点可构成直角三角形ABC，则称点C为A，B两点的勾股点．同样，点D也是A，B两点的勾股点如图1，矩形ABCD中，AB＝3，BC＝1，请在边CD上作出A，B两点（除C,D以外）的勾股点（要求：尺规作图，保留作图痕迹，不要求写作法）．
（1）如图2，矩形ABCD中，
AB＝12cm，BC＝4 cm，DM＝8 cm，AN＝5 cm．动点P从D点出发沿着DC方向以1 cm／s的速度向右移动，过点P的直线l平行于BC，当点P运动到点M时停止运动．设运动时间为t(s) ，点H为M，N两点的勾股点，且点H在直线l上．
①当t＝4，求PH的长．
②探究满足条件的点H的个数（直接写出点H的个数及相应t的取值范围，不必证明）．
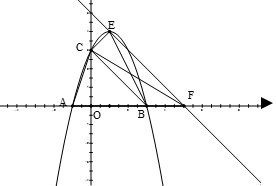
在平面直角坐标系中，已知抛物线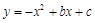
与
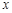轴交于点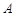
(-1,0)、
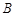(3,0)，与
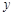轴的正半轴交于点
，顶点为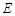
.
求抛物线解析式及顶点
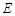的坐标；如图，过点E作BC平行线，交
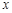轴于点F，在不添加线和字母情况下，图中面积相等的三角形有：．将抛物线向下平移，与
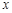轴交于点M、N，与轴的正半轴交于点P，顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP，求此时直线PN的解析式
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．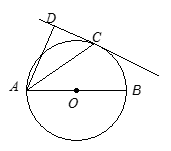
求证：AD⊥DC
若
，
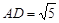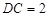，求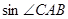
的值以及AB的长．