已知实数a≠0,函数f(x)=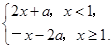
(1) 若a=-3,求f(10),f(f(10))的值;
(2) 若f(1-a)=f(1+a),求a的值.
(本小题共13分)
已知函数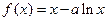 ,
,
(Ⅰ)若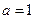 ,求函数
,求函数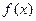 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若在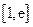 (
(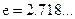 )上存在一点
)上存在一点 ,使得
,使得
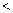
 成立,求
成立,求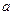 的取值范围
的取值范围
(本小题共13分)
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(Ⅰ) 随机选取1件产品,求能够通过检测的概率;
(Ⅱ)随机选取3件产品,其中一等品的件数记为 ,求
,求 的分布列;
的分布列;
(Ⅲ)随机选取3件产品,求这三件产品都不能通过检测的概率.
(本小题共14分)
在如图的多面体中, ⊥平面
⊥平面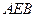 ,
,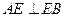 ,
, ,
, ,
, ,
, ,
,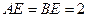 ,
, 是
是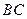 的
的 中点.
中点.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: ;
;
(Ⅲ) 求二面角 的余弦值.
的余弦值.
(本小题共13分)
在 中,内角A、B、C所对的边分别为
中,内角A、B、C所对的边分别为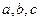 ,已知
,已知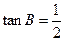 ,
, ,且
,且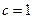 .
.
(Ⅰ)求 ;
;
(Ⅱ)求 的面积.
的面积.
已知 函数
函数 的图象在y轴上的截距为
的图象在y轴上的截距为 ,
,
相邻的两个最值点是 和
和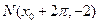
(1)求函数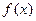 ;
;