甲厂以x千克/小时的速度运输生产某种产品(生产条件要求1≤x≤10),每小时可获得利润是100(5x+1-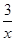 )元.
)元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点,求:
(Ⅰ)D1E与平面BC1D所成角的大小;
(Ⅱ)二面角D-BC1-C的大小;
(Ⅲ)异面直线B1D1与BC1之间的距离.
已知棱长为1的正方体AC1,E、F分别是B1C1、C1D的中点.
(1)求证:E、F、D、B共面;
(2)求点A1到平面的BDEF的距离;
(3)求直线A1D与平面BDEF所成的角.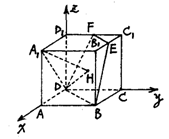
在四棱锥P—ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.
(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)求异面直线AE与CD所成角的余弦值.
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F、M分别是A1C1、A1D和B1A上任一点,求证:平面A1EF∥平面B1MC.
已知棱长为1的正方体ABCD-A1B1C1D1,求平面A1BC1与平面ABCD所成的二面角的大小