某学校拟建一块周长为400m的操场,如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?
在2008年春运期间,一名大学生要从广州回到郑州老家有两种选择,即坐火车或汽车。已知该大学生先去买火车票的概率是先去买汽车票概率的3倍,汽车票随时都能买到。若先去买火车票,则买到火车票的概率为0.6,买不到火车票,再去买汽车票。
(I)求这名大学生先去买火车票的概率;
(II)若火车票的价格为120元,汽车票的价格为280元,设该大学生购买车票所花费钱数为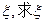 的期望值。
的期望值。
(新华网)反兴奋剂的大敌、服药者的宠儿——HGH(人体生长激素),有望在2008年8月的北京奥运会上首次“伏法”。据悉,国际体育界研究近10年仍不见显著成效的HGH检测,日前已取得新的进展,新生产的检测设备有希望在北京奥运会上使用.若组委会计划对参加某项比赛的12名运动员的血样进行突击检查,采用如下化验方法:将所有待检运动员分成若干小组,每组m个人,再把每个人的血样分成两份,化验时将每个小组内的m个人的血样各一份混合在一起进行化验,若结果中不含HGH成分,那么该组的m个人只需化验这一次就算检验合格;如果结果中含有HGH成分,那么需要对该组进行再次检验,即需要把这m个人的另一份血样逐个进行化验,才能最终确定是否检验合格,这时,对这m个人一共需要进行m+1次化验.假定对所有人来说,化验结果中含有HGH成分的概率均为  .当m=3时,求:
.当m=3时,求:
(1)一个小组只需经过一次检验就合格的概率;
(2)至少有两个小组只需经过一次检验就合格的概率(精确到0.01.参考数据:0.2713≈0.020,0.2714≈0.005,0.7292≈0.500)
已知某车间正常生产的某种零件的尺寸满足正态分布N(27.45,0.052),质量检验员随机抽查了10个零件,测得它们的尺寸为:27.34 、27.49、27.55、27.23、27.40、27.46、27.38、 27.58、 27.54、 27.68  请你根据正态分布的小概率事件,帮助质量检验员确定哪些零件应该判定在非正常状态下生产的
请你根据正态分布的小概率事件,帮助质量检验员确定哪些零件应该判定在非正常状态下生产的 
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
如果随机变量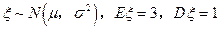 ,则
,则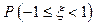 等于()
等于()
A.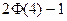 |
B.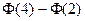 |
C.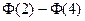 |
D.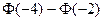 |