已知数列{an}是首项为1,公差为d的等差数列,数列{bn}是首项为1,公比为q(q>1)的等比数列.
(1)若a5=b5,q=3,求数列{an·bn}的前n项和;
(2)若存在正整数k(k≥2),使得ak=bk.试比较an与bn的大小,并说明理由..
(本小题满分13分)
在锐角 中,角
中,角 ,
,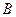 ,
, 所对的边分别为
所对的边分别为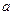 ,
, ,
, .已知
.已知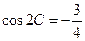 .
.
(Ⅰ)求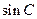 ;
;
(Ⅱ)当 ,且
,且 时,求
时,求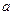 .
.
本小题满分10分)选修4-5,不等式选讲
已知 ,且
,且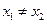 .求证:|
.求证:| .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知圆C的参数方程为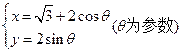 ,若P是圆C与y轴正半轴的交点,以圆心C为
,若P是圆C与y轴正半轴的交点,以圆心C为
极点,x轴的正半轴为极轴建立极坐标系,求过点P的圆C的切线的极坐标方程.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,在直径是AB的半圆上有两个不同的点M、N,设AN与BM的交点是P.
求证: .
.
(本小题满分12分)
已知函数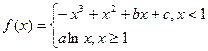
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是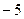 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求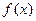 在区间
在区间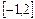 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线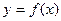 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得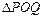 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由。
轴上?说明理由。