设无穷数列{an}满足:n∈Ν,an<an+1,an∈N.记bn=aan,cn=aan+1(n∈N*).
(1)若bn=3n(n∈N*),求证:a1=2,并求c1的值;
(2)若{cn}是公差为1的等差数列,问{an}是否为等差数列,证明你的结论.
如图,在三棱锥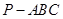 中,
中,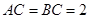 ,
,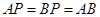 ,
,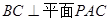 .
.
(Ⅰ)求证: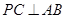 ;
;
(Ⅱ)求二面角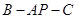 的正弦值.
的正弦值.
已知角 、
、 、
、 是
是 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量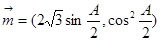 ,
, ,
,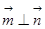 .
.
(1)求角 的大小;
的大小;
(2)若 求
求 的长.
的长.
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表
如下:
| 分组(重量) |
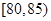 |
 |
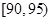 |
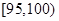 |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在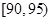 的频率;
的频率;
(2)用分层抽样的方法从重量在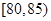 和
和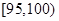 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在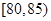 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在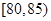 和
和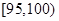 中各有1个的概率.
中各有1个的概率.
设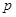 :实数
:实数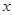 满足
满足 ;
;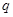 :实数
:实数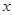 满足
满足 ,其中
,其中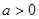 .
.
(1)若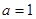 ,且
,且 为真,求实数
为真,求实数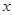 的取值范围;
的取值范围;
(2)若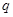 是
是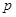 的充分不必要条件,求实数
的充分不必要条件,求实数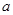 的取值范围.
的取值范围.
已知过点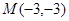 的直线
的直线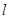 与圆
与圆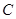 :
: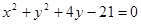 相交于
相交于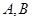 两点,若弦
两点,若弦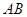 的长为
的长为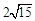 ,求直线
,求直线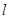 的方程.
的方程.