(本小题满分14分)设 为数列
为数列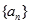 的前
的前 项和,对任意的
项和,对任意的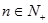 ,都有
,都有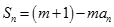
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列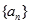 的公比
的公比 ,数列
,数列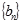 满足
满足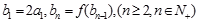 ,求数列
,求数列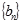 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和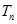 .
.
(本小题满分12分)根据公安部最新修订的《机动车驾驶证申领和使用规定》:每位驾驶证申领者必须通过《科目一》(理论科目)、《综合科》(驾驶技能加科目一的部分理论)的考试.已知李先生已通过《科目一》的考试,且《科目一》的成绩不受《综合科》的影响,《综合科》三年内有5次预约考试的机会,一旦某次考试通过,便可领取驾驶证,不再参加以后的考试,否则就一直考到第5次为止.设李先生《综合科》每次参加考试通过的概率依次为0.5,0.6,0.7,0.8,0.9.
(1)求在三年内李先生参加驾驶证考试次数 的分布列和数学期望;
的分布列和数学期望;
(2)求李先生在三年内领到驾驶证的概率.
【改编】已知向量 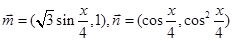 ,记
,记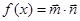
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)将函数  的图象向右平移
的图象向右平移 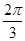 个单位得到
个单位得到 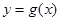 的图象,若函数
的图象,若函数 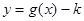 在
在 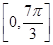 上有零点,求实数k的取值范围.
上有零点,求实数k的取值范围.
(本小题满分14分)在平面直角坐标系xOy中,椭圆C: (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为 .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
(本小题满分14分)已知函数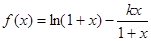 ,
, .
.
(1)讨论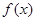 的单调区间;
的单调区间;
(2)当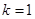 时,求
时,求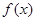 在
在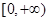 上的最小值,并证明
上的最小值,并证明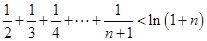 .
.