(本小题满分14分)设 为数列
为数列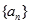 的前
的前 项和,对任意的
项和,对任意的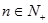 ,都有
,都有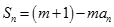
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列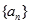 的公比
的公比 ,数列
,数列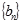 满足
满足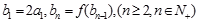 ,求数列
,求数列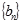 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和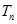 .
.
 中,角
中,角 所对的边分别为
所对的边分别为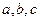 且
且 (1)求角的
(1)求角的 大小(2)若向量
大小(2)若向量 ,向量
,向量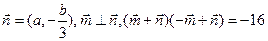 ,求
,求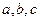 的值
的值
将数字 分别写在大小、形状都相同的
分别写在大小、形状都相同的 张卡片上,将它们反扣后(数字向下),再从左到右随机的依次摆放,然后从左到右依次翻卡片:若第一次就翻出数字
张卡片上,将它们反扣后(数字向下),再从左到右随机的依次摆放,然后从左到右依次翻卡片:若第一次就翻出数字 则停止翻卡片;否则就继续翻,若将翻出的卡片上的数字依次相加所得的和是
则停止翻卡片;否则就继续翻,若将翻出的卡片上的数字依次相加所得的和是 的倍数则停止翻卡片;否则将卡片依次翻完也停止翻卡片.设翻卡片停止时所翻的次数为随机变量
的倍数则停止翻卡片;否则将卡片依次翻完也停止翻卡片.设翻卡片停止时所翻的次数为随机变量 ,求出
,求出 的分布列和它的数学期望.
的分布列和它的数学期望.
(本题满分12分) 直角三角形 的直角顶点
的直角顶点 为动点,
为动点,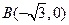 ,
,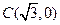 为两个定点,作
为两个定点,作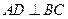 于
于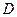 ,动点
,动点 满足
满足 ,当点
,当点 运动时,设点
运动时,设点 的轨迹为曲线
的轨迹为曲线 ,曲线
,曲线 与
与 轴正半轴的交点为
轴正半轴的交点为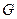 .(Ⅰ) 求曲线
.(Ⅰ) 求曲线 的方程;(Ⅱ) 是否存在方向向量为m
的方程;(Ⅱ) 是否存在方向向量为m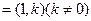 的直线
的直线 ,与曲线
,与曲线 交于
交于 ,
, 两点,使
两点,使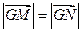 ,且
,且 与
与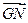 的夹角为
的夹角为 ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
(本题满分14分)设直线 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有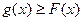 . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数 .求证:
.求证: 为曲线
为曲线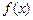 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
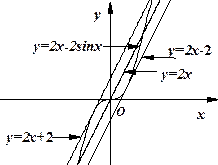
根据上图,试推测曲线 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
(本题满分12分)设 .数列
.数列 满足
满足 .(1)求证:
.(1)求证: 是等差数列;
是等差数列;
(2)求证: