(本小题满分14分)在平面直角坐标系xOy中,椭圆C: (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为 .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
(本小题满分14分)
(1)求过点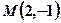 且与圆
且与圆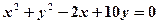 同心的圆C的方程,
同心的圆C的方程,
(2)求圆C过点 的切线方程。
的切线方程。
(本小题满分12分)
已知命题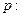 方程
方程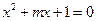 有两个不相等的实根;
有两个不相等的实根;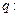 不等式
不等式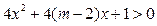 的解集为
的解集为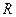 ,若
,若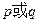 为真,且
为真,且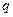 为假,求实数
为假,求实数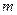 的取值范围
的取值范围
(本小题满分12分)
直线L1: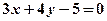 与直线L2:
与直线L2: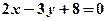 的交点为
的交点为
(1) 求经过点 和原点的直线方程;
和原点的直线方程;
(2)求经过点 与直线
与直线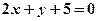 垂直的直线方程。
垂直的直线方程。
设函数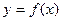 的定义域为全体R,当x<0时,
的定义域为全体R,当x<0时, ,且对任意的实数x,y∈R,有
,且对任意的实数x,y∈R,有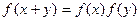 成立,数列
成立,数列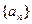 满足
满足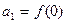 ,且
,且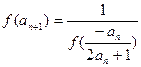 (n∈N*)
(n∈N*)
(Ⅰ)求证: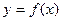 是R上的减函数;
是R上的减函数;
(Ⅱ)求数列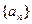 的通项公式;
的通项公式;
(Ⅲ)若不等式 对一切n∈N*均成立,求k的最大值.
对一切n∈N*均成立,求k的最大值.
如图,直角梯形ABCD,∠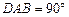 ,AD∥BC,AB=2,AD=
,AD∥BC,AB=2,AD=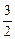 ,BC=
,BC=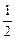 椭圆F以A、B为焦点且过点D,
椭圆F以A、B为焦点且过点D,
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
( Ⅱ)若点E满足
Ⅱ)若点E满足 ,是否存在斜率
,是否存在斜率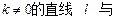
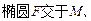
 两点,且
两点,且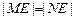 ,若存在,求K的取值范围;若不存在,说明理由。
,若存在,求K的取值范围;若不存在,说明理由。