如图,直角梯形ABCD,∠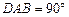 ,AD∥BC,AB=2,AD=
,AD∥BC,AB=2,AD=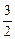 ,BC=
,BC=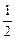 椭圆F以A、B为焦点且过点D,
椭圆F以A、B为焦点且过点D,
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
( Ⅱ)若点E满足
Ⅱ)若点E满足 ,是否存在斜率
,是否存在斜率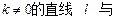
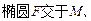
 两点,且
两点,且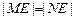 ,若存在,求K的取值范围;若不存在,说明理由。
,若存在,求K的取值范围;若不存在,说明理由。
已知动圆 过定点(1,0),且与直线
过定点(1,0),且与直线 相切.
相切.
(1)求动圆圆心 的轨迹方程;
的轨迹方程;
(2)设 是轨迹
是轨迹 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和 的倾斜角分别为
的倾斜角分别为 和
和 ,①当
,①当 时,求证直线
时,求证直线 恒过一定点
恒过一定点 ;
;
②若 为定值
为定值 ,直线
,直线 是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
如图,直角梯形 中,
中, ,点
,点 分别是
分别是 的中点,点
的中点,点 在
在 上,沿
上,沿 将梯形
将梯形 翻折,使平面
翻折,使平面
 平面
平面 .
.
(1)当 最小时,求证:
最小时,求证: ;
;
(2)当 时,求二面角
时,求二面角 平面角的余弦值.
平面角的余弦值.
已知函数 .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)设 的内角
的内角 的对应边分别为
的对应边分别为 ,且
,且 若向量
若向量 与向量
与向量 共线,求
共线,求 的值.
的值.
在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
规定:当产品中的此种元素含量 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数 的分布列及数学期望
的分布列及数学期望 .
.
已知函数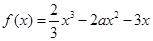 .
.
(1)当 时,求曲线
时,求曲线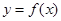 在点
在点 的切线方程;
的切线方程;
(2)对一切 ,
, 恒成立,求实数
恒成立,求实数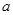 的取值范围;
的取值范围;
(3)当 时,试讨论
时,试讨论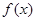 在
在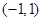 内的极值点的个数.
内的极值点的个数.