（本小题满分15分）平面直角坐标系xOy中，已知⊙M经过点F1（0，－c），F2（0，c），A（
c，0）三点，其中c＞0．
（1）求⊙M的标准方程（用含
的式子表示）；
（2）已知椭圆
（其中
）的左、右顶点分别为D、B，
⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．
①求椭圆离心率的取值范围；
②若A、B、M、O、C、D（O为坐标原点）依次均匀分布在x轴上，问直线MF1与直线DF2的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．
某市今年11份曾发生H1N1流感，据统计，11月1日该市流感病毒感染者有20人，此后，每天的新感染者平均比前一天的新感染者增加50人，由于该市医疗部门采取措施，使该种病毒的传播得到控制，从某天起，每天的新感染者平均比前一天的新感染者减少30人，到11月30日止，该市在这30日内感染该病毒的患者总共8670人，问11月几日，该市感染此病毒的新患者人数最多？并求这一天的新患者人数.
已知数列
是等差数列， 
；数列
的前n项和是
，且
．
(Ⅰ) 求数列的通项公式；
(Ⅱ) 求证：数列是等比数列；
(Ⅲ) 记
，求
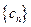的前n项和
．
某县位于沙漠地带，人与自然长期进行着顽强的斗争，到2009年底全县的绿化率已达30%。从2010年开始，每年将出现这样的局面，即原有沙漠面积的16%将被绿化，与此同时，由于各种原因，原有绿化面积的4%又被沙化。
(1)设全县面积为1，2001年底绿化面积为a1＝，经过n年绿化总面积为an＋1。
求证：an＋1＝＋an
(2)至少需要多少年(年取整数，lg2＝0.3010)的努力，才能使全县的绿化率达到60%？
已知f（x+1）=x2－4，等差数列{an}中，a1=f（x－1）， a2=－
，a3=f（x）．
（1）求x值；
（2）求a2+a5+a8+…+a26的值．
已知数列
满足
，
。
（1）求数列的通项公式；
（2）求使得
的正整数
的集合M。