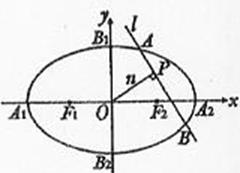
如图,椭圆C: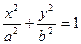 的顶点为A1,A2,B1,B2,焦点为F1,F2,,
的顶点为A1,A2,B1,B2,焦点为F1,F2,,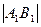 =
= 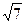 ,
,

(Ⅰ)求椭圆C的方程;
(Ⅱ)设n是过原点的直线,l是与n垂直相交于P点、与椭圆相交于A,B两点的直线, ,是否存在上述直线l使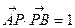 成立?若存在,求出直线l的方程;若不存在,请说明理由。
成立?若存在,求出直线l的方程;若不存在,请说明理由。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金为多少元时,租凭公司有月收益最大?最大月收益是多少元?
已知函数f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1.
(Ⅰ)若函数f(x)在x=-2处有极值,求f(x)的表达式;
(Ⅱ)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围.
如图,在五面体ABCDEF中,FA  平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=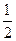 AD
AD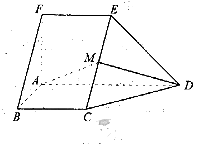
(1)证明平面AMD 平面CDE;
平面CDE;
(2)求二面角A-CD-E的余弦值
已知
的角
、
、
所对的边分别是
、
、
,设向量
,
,
.
(1)若
,求证:
为等腰三角形;
(2)若
,边长
,角
,求
的面积.
设函数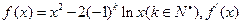 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{ }满足
}满足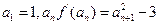 .证明:数列{
.证明:数列{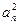 }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有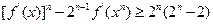 成立.
成立.