已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
如图,射线OA,OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在直线y= x上时,求直线AB的方程.
x上时,求直线AB的方程.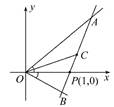
已知函数 ,
, (
( ,
, ).
).
(1)判断曲线 在点(1,
在点(1, )处的切线与曲线
)处的切线与曲线 的公共点个数;
的公共点个数;
(2)当 时,若函数
时,若函数 有两个零点,求
有两个零点,求 的取值范围.
的取值范围.
已知椭圆 :
: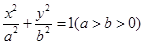 的离心率为
的离心率为 ,右焦点
,右焦点 到直线
到直线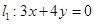 的距离为
的距离为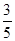 .
.
(1)求椭圆 的方程;
的方程;
(2)过椭圆右焦点F2斜率为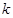 (
( )的直线
)的直线 与椭圆
与椭圆 相交于
相交于 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线 于点
于点 ,线段
,线段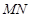 的中点为
的中点为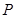 ,记直线
,记直线 的斜率为
的斜率为 ,求证:
,求证: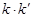 为定值.
为定值.
在数列 中,
中, ,
,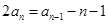
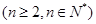 ,设
,设 .
.
(1)证明:数列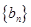 是等比数列;
是等比数列;
(2)求数列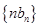 的前
的前 项和
项和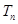 ;
;
(3)若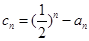 ,
, 为数列
为数列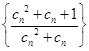 的前
的前 项和,求不超过
项和,求不超过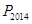 的最大的整数.
的最大的整数.
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
(1)求参加数学抽测的人数 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在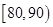 ,
, 内的人数;
内的人数;
(2)若从分数在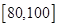 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在 内的概率.
内的概率.