在平面直角坐标系中,已知点 和
和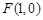 ,圆
,圆 是以
是以 为圆心,半径为
为圆心,半径为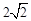 的圆,点
的圆,点 是圆
是圆 上任意一点,线段
上任意一点,线段 的垂直平分线
的垂直平分线 和半径
和半径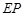 所在的直线交于点
所在的直线交于点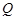 .
.
(1)当点 在圆上运动时,求点
在圆上运动时,求点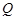 的轨迹方程
的轨迹方程 ;
;
(2)已知 ,
, 是曲线
是曲线 上的两点,若曲线
上的两点,若曲线 上存在点
上存在点 ,满足
,满足 (
(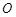 为坐标原点),求实数
为坐标原点),求实数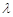 的取值范围.
的取值范围.
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽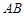 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(1)求水面宽;
(2)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
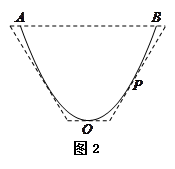
(3)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
如图,已知 的直径
的直径 ,点
,点 、
、 为
为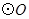 上两点,且
上两点,且 ,
, ,
,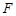 为弧
为弧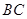 的中点.将
的中点.将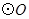 沿直径
沿直径 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).
(1)求证: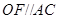 ;
;
(2)在弧 上是否存在点
上是否存在点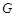 ,使得
,使得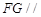 平面
平面 ?若存在,试指出点
?若存在,试指出点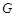 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;
(3)求二面角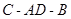 的正弦值.
的正弦值.
已知函数 的部分图象如图所示,其中点A为最高点,点B,C为图象与轴的交点,在
的部分图象如图所示,其中点A为最高点,点B,C为图象与轴的交点,在 中,角
中,角 对边为
对边为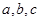 ,
, ,且满足
,且满足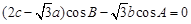 .
.
(1)求 的面积;
的面积;
(2)求函数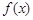 的单调递增区间.
的单调递增区间.
已知函数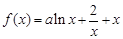 ,其中
,其中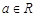 .
.
(1)若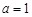 ,求函数
,求函数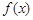 的极值点;
的极值点;
(2)若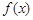 在区间
在区间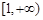 内单调递增,求实数
内单调递增,求实数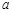 的取值范围.
的取值范围.