如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.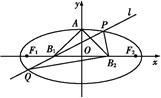
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
(本小题共13分)设数列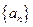 的前
的前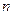 项和
项和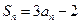
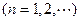 .
.
(Ⅰ)证明数列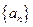 是等比数列;
是等比数列;
(Ⅱ)若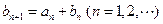
 ,且
,且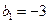 ,求数列
,求数列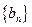 的前
的前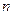 项和
项和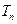
(本小题满分13分)已知圆C: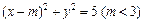 过点A(3,1),且过点(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
过点A(3,1),且过点(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
(1)求切线PF的方程;
(2)若抛物线E的焦点为F,顶点在原点,求抛物线E的方程。
(3)若Q为抛物线E上的一个动点,求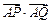 的取值范围.
的取值范围.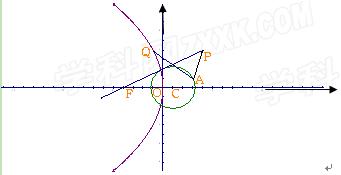
(本小题满分13分)已知函数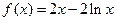

(Ⅰ)求函数在点(1, 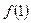 )处的切线方程
)处的切线方程
(Ⅱ)求函数 的极值
的极值
(Ⅲ)对于曲线上的不同两点 ,如果存在曲线上的点
,如果存在曲线上的点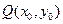 ,且
,且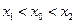 ,使得曲线在点
,使得曲线在点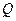 处的切线
处的切线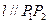 ,则称
,则称 为弦
为弦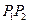 的陪伴切线.已知两点
的陪伴切线.已知两点
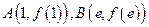 ,试求弦
,试求弦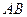 的陪伴切线
的陪伴切线 的方程;
的方程;
如图是某直三 棱柱(侧棱与底面垂直)被削去上底后的
棱柱(侧棱与底面垂直)被削去上底后的
直观图与三视图的侧视图、俯视图,在直观图中,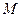 是
是
 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.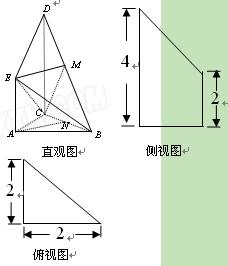
(Ⅰ)求出该 几何体的体积。
几何体的体积。
(Ⅱ)若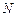 是
是
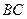 的中点,求证:
的中点,求证: 平面
平面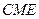 ;
;
(Ⅲ)求证:平面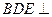 平面
平面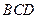 .
.
(本小题满分12分)根据市气象站 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(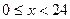 ,单位为小时,
,单位为小时,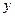 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
, ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。