如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.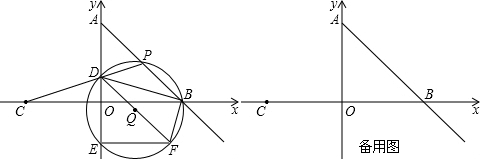
(1)求直线AB的函数解析式;
(2)当点P在线段AB(不包括A,B两点)上时.
①求证:∠BDE=∠ADP;
②设DE=x,DF=y.请求出y关于x的函数解析式;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.
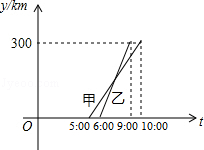
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:
(1)A、B两城之间距离是多少千米?
(2)求乙车出发多长时间追上甲车?
(3)直接写出甲车出发多长时间,两车相距20千米.
某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
如图,二次函数 的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数 的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足 的x的取值范围.

如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求出在这两次变换过程中,点A经过点A1到达A2的路径总长.

先化简,再求值: ,其中 .