如图，在三棱锥SABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB，过A作AF⊥SB，垂足为F，点E、G分别是棱SA、
SC的中点．求证：
(1)平面EFG∥平面ABC；
(2)BC⊥SA.
已知函数f(x)=|x-1|+|x+3|.
(1)求x的取值范围,使f(x)为常数函数.
(2)若关于x的不等式f(x)-a≤0有解,求实数a的取值范围.
设函数f(x)=|2x-1|+|2x-3|,x∈R.
(1)求关于x的不等式f(x)≤5的解集.
(2)若g(x)=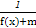
的定义域为R,求实数m的取值范围.
设函数f(x)=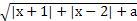
.
(1)当a=-5时,求函数f(x)的定义域.
(2)若函数f(x)的定义域为R,试求a的取值范围.
设f(x)=
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
关于x的不等式|x-3|+|x-4|<a的解集不是空集,求a的取值范围.