如图,直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.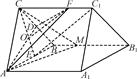
(1)求证:C1E∥平面ADF;
(2)设点M在棱BB1上,当BM为何值时,平面CAM⊥平面ADF?
已知数列 、
、 满足:
满足: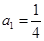 ,
, ,
, 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列{
,求数列{ }的前n项和
}的前n项和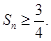
在如图所示的几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF//AB,AF⊥CF。
(Ⅰ)若G为FC的中点,证明:AF//平面BDG;
(Ⅱ)求平面ABF与平面BCF夹角的余弦值。
在 中,
中, 分别为角
分别为角 的对边,且
的对边,且
(Ⅰ)求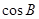 ;
;
(Ⅱ)若 ,点
,点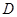 是线段
是线段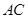 中点,且
中点,且 ,若角
,若角 大于
大于 ,求
,求 的面积.
的面积.
已知函数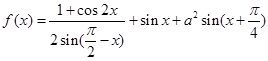
(Ⅰ)求函数y = f(x)的单调递增区间;
(Ⅱ)当x∈[0,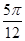 ] 时,函数y=f(x)的最小值为
] 时,函数y=f(x)的最小值为 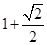 ,试确定常数a的值.
,试确定常数a的值.
已知等差数列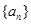 满足:
满足: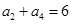 ,
,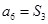 ,其中
,其中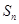 为数列
为数列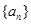 的前n项和.
的前n项和.
(Ⅰ)求数列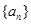 的通项公式;
的通项公式;
(Ⅱ)若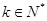 ,且
,且 成等比数列,求
成等比数列,求 的值。
的值。