已知f(n)＝1＋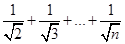
n∈N)，g(n)＝2(
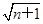－1)(n∈N)．
(1)当n＝1，2，3时，分别比较f(n)与g(n)的大小(直接给出结论)；
(2)由(1)猜想f(n)与g(n)的大小关系，并证明你的结论．
已知正数a、b、c满足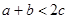
，求证：
在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系曲线C的极坐标方程为cos（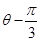
）=1，M,N分别为C与x轴，y轴的交点。
（I）写出C的直角坐标方程，并求M,N的极坐标；
（II）设MN的中点为P，求直线OP的极坐标方程。
已知函数
.
（Ⅰ）讨论函数
的单调性；
（Ⅱ）设
，证明：对任意
，
.
过点C(0，1)的椭圆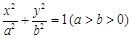
的离心率为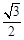
，椭圆与x轴交于两点
、
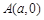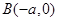，过点C的直线
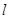与椭圆交于另一点D，并与x轴交于点P，直线AC与直线BD交于点Q．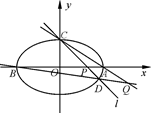
（I）当直线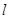过椭圆右焦点时，求线段CD的长；
（II）当点P异于点B时，求证：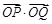
为定值．
如图，在直四棱柱
中，已知
，
．
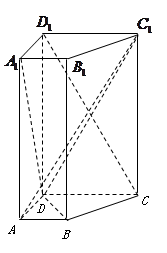
（Ⅰ）求证：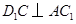
；
（Ⅱ）设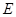
是
上一点，试确定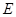的位置，使
平面
，并说明理由．