设数列{an}：1，－2，－2，3，3，3，－4，－4，－4，－4，…，(－1)k－1k，…，(－1)
，即当
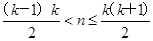(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)，用数学归纳法证明Si(2i＋1)＝－i(2i＋1)(i∈N*)．
（理）设函数
,其中
。
（Ⅰ）当
时，求不等式
的解集；
（Ⅱ）若不等式
的解集为
，求a的值。
叙述并证明余弦定理．
。函数y＝Asin（ωx+φ）（A＞0,ω＞0）在x∈（0，7π）内取到一个
最大值和一个最小值，且当x＝π时，y有最大值3，当x＝6π时，y有最小值-3．
（1）求此函数解析式；
（2）是否存在实数ω，满足Asin（ω
+φ）＞Asin（ω
+φ）?若存在，求出m．若不存在，说明理由．
在
中，角
所对的边分别为
，且满足
．
（I）求角
的大小；
（II）求
的最大值，并求取得最大值时角
的大小．
为进行科学实验，观测小球A、B在两条相交成
角的直线型轨道上
运动的情况，如图（乙）所示，运动开始前，A和B分别距O点3m和1m，后来它们同时
以每分钟4m的速度各沿轨道
按箭头的方向运动。问：
（1）运动开始前，A、B的距离是多少米？（结果保留三位有效数字）。
（2）几分钟后，两个小球的距离最小？