如图,圆锥的高PO=4,底面半径OB=2,D为PO的中点,E为母线PB的中点,F为底面圆周上一点,满足EF⊥DE.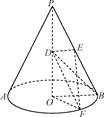
(1)求异面直线EF与BD所成角的余弦值;
(2)求二面角OOFE的正弦值.
有两颗正四面体的玩具,其四个面上分别标有数字 ,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
(1)求事件“点数之和不小于4”的概率;
(2)求事件“点数之积能被 或
或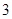 整除”的概率.
整除”的概率.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
(1)写出评委为乙选手打出分数数据的众数,中位数;
(2)求去掉一个最高分和一个最低分后,两位选手所剩数据的平均数和方差,根据结果比较,哪位选手的数据波动小?
已知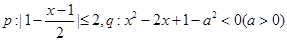 ,
,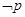 是
是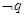 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
函数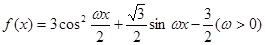 在一个周期内的图象如图所示,
在一个周期内的图象如图所示,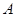 为图象的最高点,
为图象的最高点, 、
、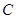 为图象与
为图象与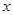 轴的交点,且
轴的交点,且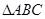 为等边三角形。将函数
为等边三角形。将函数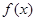 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的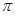 倍,将所得图象向右平移
倍,将所得图象向右平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数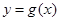 的图象
的图象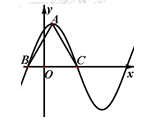
(1)求函数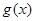 的解析式及函数
的解析式及函数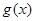 的对称中心.
的对称中心.
(2)若 对任意
对任意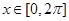 恒成立,求实数
恒成立,求实数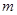 的取值范围。
的取值范围。
已知在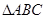 中,
中,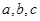 分别是角
分别是角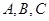 的对边,,且满足
的对边,,且满足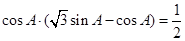
(1)求角 的大小; (2)若
的大小; (2)若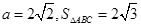 ,求
,求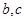 的长。
的长。