在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
(1)求二面角D1-AE-C的大小;
(2)求证:直线BF∥平面AD1E.
选修4-4:坐标系与参数方程
在直角坐标版权法
吕,直线
的参数方程为
(
为参数),以原点为极点,
轴的正半轴为极轴建立极坐标系,
的极坐标方程为
.
(Ⅰ)写出
的直角坐标方程;
(Ⅱ)
为直线
上一动点,当
到圆心
的距离最小时,求点
的坐标.
如图,
切
于点
,直线
交
于
两点,
垂足为
.
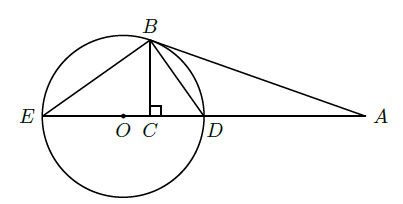
(Ⅰ)证明:
(Ⅱ)若 ,求 的直径.
设 .
(Ⅰ)求
;
(Ⅱ)证明:
在
内有且仅有一个零点(记为
),且
.
如图,椭圆
经过点
,且离心率为
.
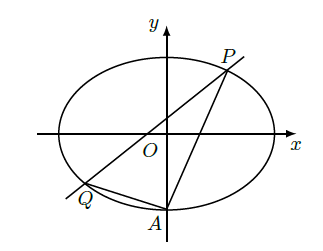
(Ⅰ)求椭圆
的方程;
(Ⅱ)经过点 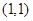 ,且斜率为
的直线与椭圆
交于不同两点
(均异于点
),证明:直线
与
的斜率之和为2.
,且斜率为
的直线与椭圆
交于不同两点
(均异于点
),证明:直线
与
的斜率之和为2.
随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
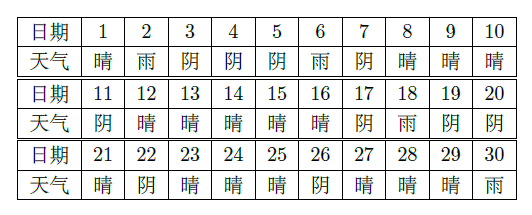
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.