如图,已知点D(0,-2),过点D作抛物线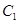 :
: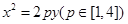 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。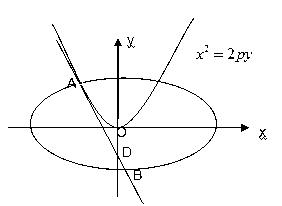
(1)求切点A的纵坐标;
(2)若离心率为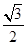 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k, ,①试用斜率k表示
,①试用斜率k表示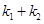 ②当
②当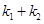 取得最大值时求此时椭圆的方程。
取得最大值时求此时椭圆的方程。
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层,…,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第 层第
层第 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第 层的第
层的第 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.
(Ⅰ)试求 及
及 的值,并猜想
的值,并猜想 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中 ,试求
,试求 的分布列
的分布列
及数学期望.
已知A、B、C为 的三个内角且向量
的三个内角且向量 共线。
共线。
(Ⅰ)求角C的大小;
(Ⅱ)设角 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
 的形状.
的形状.
已知区间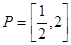 ,函数
,函数 的定义域为
的定义域为
(1)若函数在区间 上是增函数,求实数
上是增函数,求实数 的取值范围
的取值范围
(2)若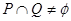 ,求实数
,求实数 的取值范围
的取值范围
(3)若关于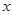 的方程
的方程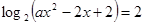 在区间
在区间 内有解,求实数
内有解,求实数 的取值范围
的取值范围
如图,某多面体的直观图及三视图如图所示: E,F分别为PC,BD的中点
(1)求证: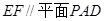
(2)求证:
(3)求此多面体的体积
直线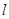 被两直线
被两直线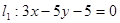 和
和 截得的线段中点为P
截得的线段中点为P
(1)求直线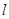 的方程
的方程
(2)已知点 ,在直线
,在直线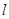 上找一点M,使
上找一点M,使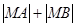 最小,并求出这个最小值
最小,并求出这个最小值