已知函数f(x)=ax2-(4a+2)x+4lnx,其中a≥0.
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
直棱柱ABCD—A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
(1)求证:平面ACB1⊥平面BB1C1C;
(2)在A1B1上是否存在一点P,使得DP与平面ACB1平行?证明你的结论.
△ABC的内角A、B、C的对边分别为a,b,c,asin A+csin C-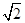 asin C=bsin B.
asin C=bsin B.
(1)求B;
(2)若A=75°,b=2,求a,c.
以下茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.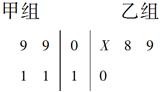
(1)如果X=8,求乙组同学植树棵数的平均数;
(2) 记甲组四名同学为A1,A2,A3,A4,乙组四名同学为B1,B2,B3,B4,如果X=9,分别从甲、乙两组中随机选取一名同学,列举这两名同学的植树总棵数为19的所有情形并求该事件的概率.
已知函数 .
.
(Ⅰ)若 无极值点,但其导函数
无极值点,但其导函数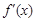 有零点,求
有零点,求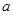 的值;
的值;
(Ⅱ)若 有两个极值点,求
有两个极值点,求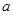 的取值范围,并证明
的取值范围,并证明 的极小值小于
的极小值小于 .
.
已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求a,b满足的关系式;
(2)若 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
(3)证明: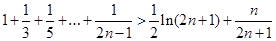 (
(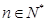 )
)