函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<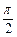 )的图象如图所示,
)的图象如图所示,
(1)求y= f(x)的表达式;
(2)若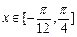 ,求y=f(x)的值域。
,求y=f(x)的值域。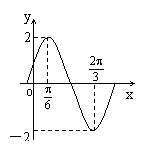
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
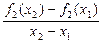 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
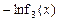 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
(本小题满分14分)已知函数  ,
, .
.
(1)当 时,求曲线
时,求曲线 在点(3,
在点(3, )处的切线方程;
)处的切线方程;
(2)当函数 在
在 上有唯一的零点时,求实数
上有唯一的零点时,求实数 的取值范围.
的取值范围.
(本小题满分14分)某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为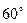 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为 平方米,且高度不低于
平方米,且高度不低于 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为 (米).
(米).
⑴求 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过 米,则其腰长
米,则其腰长 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值. 
(本小题满分14分)在平面直角坐标系中, 为坐标原点,已知向量
为坐标原点,已知向量 ,又点
,又点 .
.
(1)若 ,且
,且 ,求向量
,求向量 ;
;
(2)若向量 与向量
与向量 共线,当
共线,当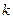
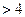 时,且
时,且 取最大值为4时,求
取最大值为4时,求 .
.