如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.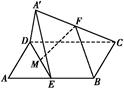
(1)求证:BF∥平面A′DE;
(2)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分其中①6分、②2分。
设抛物线
的焦点为
，过且垂直于
轴的直线与抛物线交于
两点，已知
.
（1）求抛物线
的方程；
（2）设
，过点
作方向向量为
的直线与抛物线相交于
两点，求使
为钝角时实数
的取值范围；
（3）①对给定的定点
，过作直线与抛物线相交于两点，问是否存在一条垂直于轴的直线与以线段
为直径的圆始终相切？若存在，请求出这条直线；若不存在，请说明理由。
②对
，过作直线与抛物线相交于两点，问是否存在一条垂直于轴的直线与以线段为直径的圆始终相切？（只要求写出结论，不需用证明）
本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分。
定义：对函数
，对给定的正整数
，若在其定义域内存在实数
，使得
，则称函数
为“性质函数”。
（1）判断函数
是否为“性质函数”？说明理由；
（2）若函数
为“2性质函数”，求实数
的取值范围；
（3）已知函数
与
的图像有公共点，求证：
为“1性质函数”。
本题共有2个小题，第1小题满分6分，第2小题满分8分。已知数列
是各项均不为
的等差数列，公差为
，
为其前
项和，且满足
，
．数列
满足
，
为数列的前n项和．
(1)求
、
和；
(2)若对任意的
，不等式
恒成立，求实数
的取值范围
本题共有2个小题，第1小题满分6分，第2小题满分8分。
如图，已知四棱锥P—ABCD，底面ABCD为矩形，
，PA
平面ABCD， E，F分别是BC，PC的中点。
（1）求异面直线PB与AC所成的角的余弦值；
（2）求三棱锥
的体积。
小明购买一种叫做“买必赢”的彩票，每注售价10元，中奖的概率为2％，如果每注奖的奖金为300元，那么小明购买一注彩票的期望收益是多少元？