已知以点C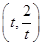 (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
(本题14分)数列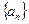 的各项均为正数,
的各项均为正数,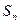 为其前
为其前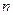 项和,对于任意
项和,对于任意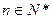 总有
总有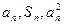 成等差数列。
成等差数列。
(1)求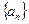 的通项公式;
的通项公式;
(2)设数列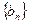 的前
的前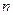 项和为
项和为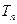 ,且
,且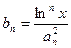 ,求证对任意的实数
,求证对任意的实数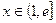 和任意的整数
和任意的整数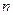 总有
总有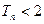 ;
;
(3)正数数列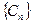 中,
中,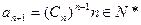 ,求数列
,求数列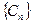 的最大项。
的最大项。
(本题13分)已知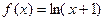 。
。
(1)若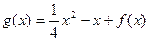 ,求
,求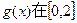 上的最大值与最小值;
上的最大值与最小值;
(2)当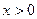 时,求证
时,求证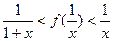 ;
;
(3)当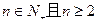 时,求证:
时,求证: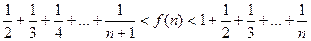
(本题12分)某汽车厂有一条价值为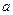 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值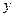 万元与技术改造投入
万元与技术改造投入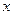 万元之间满足:①
万元之间满足:①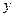 与
与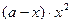 成正比;②当
成正比;②当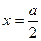 时,
时,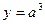 ,并且技术改造投入满足
,并且技术改造投入满足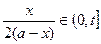 ,其中
,其中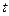 为常数且
为常数且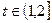 。
。
(1)求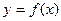 表达式及定义域;
表达式及定义域;
(2)求出产品增加值的最大值及相应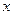 的值。
的值。
(本题12分)函数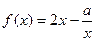 的定义域为
的定义域为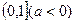 ,
,
(1)若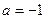 ,求函数
,求函数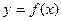 的值域;
的值域;
(2)求函数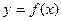 在
在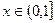 上的最大值和最小值,并求出函数取最值时相应
上的最大值和最小值,并求出函数取最值时相应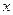 的值。
的值。
(本题12分)已知数列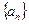 的前
的前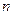 项和
项和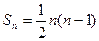 ,且
,且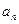 是
是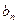 和1的等差中项。
和1的等差中项。
(1)求数列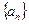 与
与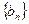 的通项公式;
的通项公式;
(2)若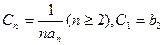 ,求
,求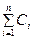 ;
;
(3)若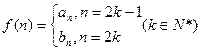 是否存在
是否存在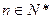 ,使
,使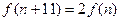 ?说明理由。
?说明理由。