江西某品牌豆腐食品是经过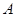
、
、
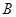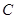三道工序加工而成的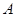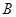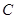，、、工序的产品合格率分别为
、
、
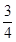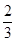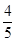．已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；恰有两次合格为二等品；其它的为废品，不进入市场．
（1）生产一袋豆腐食品，求产品为废品的概率；
（2）生产一袋豆腐食品，设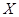
为三道加工工序中产品合格的工序数，求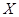的分布列和数学期望．
设函数
（I）求函数
的单调区间；
（II）若不等式
（
）在
上恒成立，求
的最大值.
设点
、
分别是椭圆
的左、右焦点,
为椭圆
上任意一点,且
的最小值为
.
（I）求椭圆的方程;
（II）设直线
（直线
、
不重合）,若、均与椭圆相切，试探究在
轴上是否存在定点
,使点到、的距离之积恒为1?若存在,请求出点坐标;若不存在,请说明理由.
如图，在几何体
中，
，
,
，且
，
.
（I）求证:
；
（II）求二面角
的余弦值.
某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙，已知从城市甲到城市乙只有两条公路，且运费由厂商承担．若厂商恰能在约定日期(×月×日)将牛奶送到，则城市乙的销售商一次性支付给牛奶厂20万元；若在约定日期前送到，每提前一天销售商将多支付给牛奶厂1万元；若在约定日期后送到，每迟到一天销售商将少支付给牛奶厂1万元．为保证牛奶新鲜度，汽车只能在约定日期的前两天出发，且只能选择其中的一条公路运送牛奶，已知下表内的信息：
| 统计信息 汽车行驶路线 |
在不堵车的情况下到达城市乙所需时间(天) |
在堵车的情况下到达城市乙所需时间(天) |
堵车的概率 |
运费(万元) |
| 公路1 |
2 |
3 |
 |
1.6 |
| 公路2 |
1 |
4 |
 |
0.8 |
（I）记汽车选择公路1运送牛奶时牛奶厂获得的毛收入为
(单位：万元)，求的分布列和数学期望
；
（II）如果你是牛奶厂的决策者，你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多？
(注：毛收入＝销售商支付给牛奶厂的费用－运费)
如图，在凸四边形
中，
为定点,
为动点，满足
.
（I）写出
与
的关系式；
（II）设
的面积分别为
和
，求
的最大值.