某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组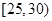 ,第2组
,第2组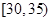 ,第3组
,第3组 ,第4组
,第4组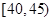 ,第5组
,第5组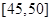 ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。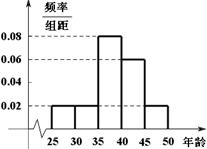
| 区间 |
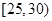 |
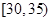 |
 |
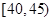 |
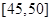 |
| 人数 |
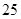 |
a |
b |
|
|
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
已知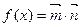 ,其
,其 中
中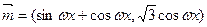 ,
,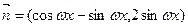
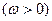 ,若
,若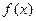 图象中相邻的对称轴间的距离不小于
图象中相邻的对称轴间的距离不小于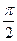 .
.
(1)求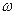 的取值范围;
的取值范围;
(2)在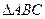 中,
中,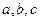 分别为角
分别为角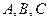 的对边.当
的对边.当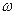 取最大值时,
取最大值时,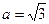 ,
,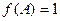 ,
,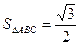 ,求此时
,求此时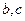 的值.
的值.
.已知函数 .
.
(1)如果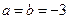 ,求
,求 的单调区间和极值;
的单调区间和极值;
(2)如果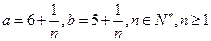 ,函数
,函数 在
在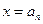 处取得极值
处取得极值 .
.
(i)求证: ;
;
(ii)求证: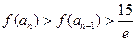 .
.
.已知中心在原点,焦点在 轴上,离心率为
轴上,离心率为 的椭圆过点(
的椭圆过点( ,
,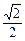 )
)
(1) 求椭圆方程;
(2) 设不过原点O的直线 ,与该椭圆交于P、Q两点,直线OP、PQ、OQ的斜率依次为
,与该椭圆交于P、Q两点,直线OP、PQ、OQ的斜率依次为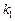 、
、 、
、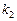 ,满足
,满足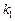 、
、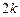 、
、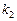 依次成等差数列,求△OPQ面积的取值范围.
依次成等差数列,求△OPQ面积的取值范围.
.如图,四棱锥P-ABCD中,PA⊥底面ABCD,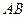 ∥
∥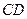 ,AD=CD=1,∠
,AD=CD=1,∠ =120°,
=120°, =
= ,∠
,∠ =90°,M是线段PD上的一点(不包括端点).
=90°,M是线段PD上的一点(不包括端点).
(1)求证:BC⊥平面PAC;
(2)求异面直线AC与PD所成的角的余弦值
(3)试确定点M的位置,使直线MA与平面PCD所成角 的正弦值为
的正弦值为 .
.
已知等比数列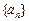 的公比大于1,
的公比大于1,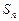 是数列
是数列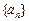 的前n项和,
的前n项和,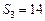 ,且
,且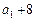 ,
,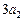 ,
,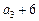 依次成等差数列,数列
依次成等差数列,数列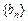 满足:
满足: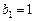 ,
,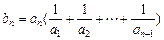
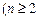 )
)
(1) 求数列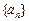 、
、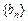 的通项公式;
的通项公式;
(2)求数列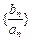 的前n项和为
的前n项和为