已知:a、b、c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2).②
∴c2=a2+b2.③
∴△ABC是直角三角形.
问:
(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ______________;
(2)错误的原因为________________________________;
(3)本题正确的解题过程:
如图, 在 中,
中,  是
是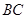 边上的一点,
边上的一点, 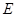 是
是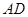 的中点, 过
的中点, 过 点作
点作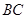 的平行线交
的平行线交 的延长线于点
的延长线于点 , 且
, 且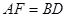 , 连接
, 连接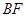 .
.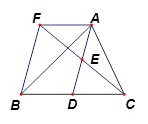
(1) 求证:  是
是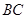 的中点;
的中点;
(2) 若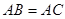 , 试判断四边形
, 试判断四边形 的形状, 并证明你的结论.
的形状, 并证明你的结论.
有三张卡片(背面完全相同)分别写有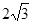 、
、 、
、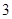 ,把它们背面朝上洗匀后,小明从中抽取一张,记下这个数后放回洗匀,小白又从中抽出一张.
,把它们背面朝上洗匀后,小明从中抽取一张,记下这个数后放回洗匀,小白又从中抽出一张.
(1)小明抽取的卡片为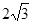 的概率是 ;两人抽取的卡片都为
的概率是 ;两人抽取的卡片都为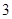 的概率是 .
的概率是 .
(2)小刚为他们俩设计了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小明获胜,否则小白获胜.你认为这个游戏规则对谁有利?请说明理由.
先化简,再求值: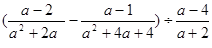 ,其中
,其中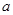 满足
满足 .
.
在直角坐标系x o y中,已知点P是反比例函数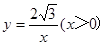 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.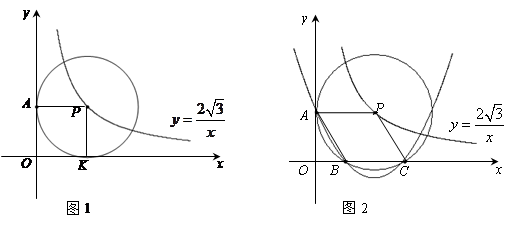
(1)如图1,⊙P运动到与x轴相切时,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 .若存在,请直接写出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,请直接写出所有满足条件的M点的坐标,若不存在,试说明理由.
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD= ,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.
,AB=6.在底边AB上有一动点E,满足∠DEQ=120°,EQ交射线DC于点F.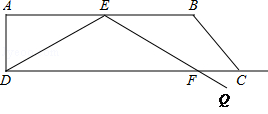
(1)求下底DC的长度;
(2)当点E是AB的中点时,求线段DF的长度;
(3)请计算射线EF经过点C时,AE的长度.