在直角坐标系x o y中，已知点P是反比例函数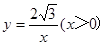
图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．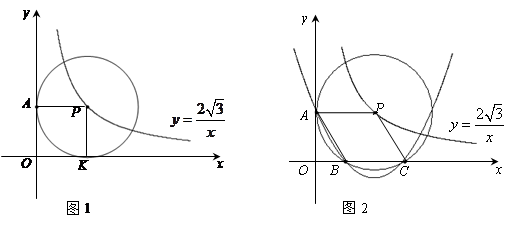
（1）如图1，⊙P运动到与x轴相切时，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的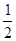
．若存在，请直接写出所有满足条件的M点的坐标，若不存在，试说明理由．
作图题：在下图中平移三角形ABC，使点A移到点D，点B和点C应移到什么位置？请在图中画出平移后图形（保留作图痕迹）．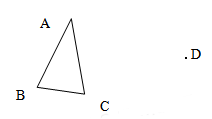
解方程：
（1）
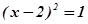
（2）
如图，长方形纸片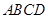
中，AB=10，将纸片折叠，使顶点
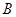落在边
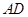上的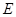
点处，折痕的一端
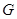点在边
上．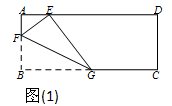
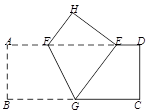
图（2）
（1）如图（1），当折痕的另一端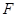
在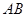
边上且AE=5时，求AF的长
（2）如图（2），当折痕的另一端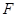在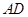边上且BG=13时，求AF的长．
如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．求证：
（1）
；
（2）
．
已知：如图，∠C=90°，BC=AC，D、E分别在BC和AC上，且BD=CE，M是AB的中点．求证：DM=EM