若盒中装有同一型号的灯泡共10只，其中有8只合格品，2只次品
（1）某工人师傅有放回地连续从该盒中取灯泡3次，每次取一只灯泡，求2次取到次品的概率；
（2）某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡，每次从中取一灯泡，若是正品则用它更换已坏灯泡，若是次品则将其报废（不再放回原盒中），求成功更换会议室的已坏灯泡所用灯泡只数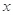
的分布列和数学期望
设数列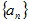
的前n项和为
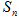，且满足
．
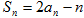（1）求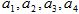
；
（2）猜想数列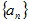的通项公式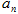
，并用数学归纳法证明
（本小题满分10分）已知函数f（x）＝ax3＋cx＋d（a≠0）是R上的奇函数，当x＝1时，f（x）取得极值－2．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间和极大值；
（本小题满分12分）已知函数
．
（Ⅰ）求函数
的单调递增区间；
（Ⅱ）证明：当
时，
；
（Ⅲ）确定实数
的所有可能取值，使得存在
，当
时，恒有
．
（本小题满分12分）已知函数
（Ⅰ）讨论函数
的单调性；
（Ⅱ）证明：若
，则对任意
，
，有
．
（本小题满分12分）已知数列
是首项为正数的等差数列，数列
的前
项和为
．
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，求数列
的前项和
．