(本小题满分12分)已知函数 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:当 时,
时, ;
;
(Ⅲ)确定实数 的所有可能取值,使得存在
的所有可能取值,使得存在 ,当
,当 时,恒有
时,恒有 .
.
设函数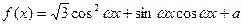 (其中
(其中 >0,
>0, ),且
),且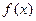 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为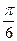 .(1)求
.(1)求 的值;(2)如果
的值;(2)如果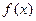 在区间
在区间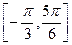 上的最小值为
上的最小值为 ,求a的值.
,求a的值.
设函数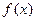 是定义在区间
是定义在区间 上以2为周期的函数,记
上以2为周期的函数,记 .已知当
.已知当 时,
时, ,如图.
,如图.
(1)求函数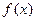 的解析式;
的解析式;
(2)对于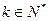 ,求集合
,求集合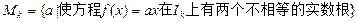 .
.
(本小题14分)已知函数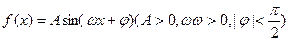 在一个周期内的图象下图所示。(1)求函数的解析式;(2)设
在一个周期内的图象下图所示。(1)求函数的解析式;(2)设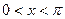 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
(本小题14分)已知函数 .
.
(1)求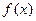 的定义域;(2)若角
的定义域;(2)若角 在第一象限且
在第一象限且 ,求
,求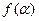 的值.
的值.
(本小题13分)已知函数

(1)用五点法画出它在一个周期
内的闭区间上的图象;
(2)指出 的周期、
的周期、
振幅、初相、对称轴;
(3)说明此函数图象可由 上的图象经
上的图象经
怎样的变换得到.