如图1,在Rt 中,
中, ,
, D、E分别是
D、E分别是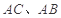 上的点,且
上的点,且 ,将
,将 沿
沿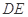 折起到
折起到 的位置,使
的位置,使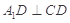 ,如图2.
,如图2.
(1)求证:平面 平面
平面 ;
;
(2)若 ,求
,求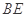 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(3)当 点在何处时,
点在何处时, 的长度最小,并求出最小值.
的长度最小,并求出最小值.
已知角 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴非负半轴重合而终边经过点
轴非负半轴重合而终边经过点 .
.
(1)求 的值;(2)求
的值;(2)求 的值.
的值.
已知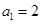 ,点
,点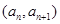 在函数
在函数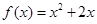 的图象上,其中
的图象上,其中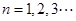
(1)证明:数列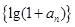 是等比数列,并求数列
是等比数列,并求数列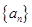 的通项公式;
的通项公式;
(2)记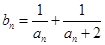 ,求数列
,求数列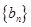 的前
的前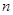 项和
项和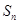 .
.
森林失火了,火正以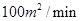 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火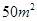 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟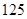 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人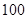 元,而每烧毁
元,而每烧毁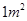 森林的损失费为
森林的损失费为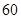 元,设消防队派了
元,设消防队派了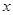 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时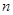
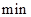 .
.
(1)求出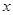 与
与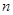 的关系式;
的关系式;
(2)问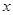 为何值时,才能使总损失最小.
为何值时,才能使总损失最小.
已知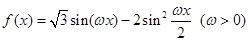 的最小正周期为
的最小正周期为 .
.
(Ⅰ)当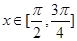 时,求函数
时,求函数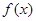 的最小值;
的最小值;
(Ⅱ)在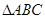 ,若
,若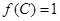 ,且
,且 ,求
,求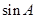 的值.
的值.
已知函数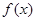 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当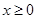 时,
时,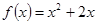 .
.
(1)写出函数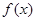 在
在 的解析式;
的解析式;
(2)若函数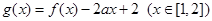 ,求函数
,求函数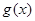 的最小值.
的最小值.