4500人按有无吸烟史和是否患高血压,分类得到列联表如下。画出柱形图,检验吸烟与患高血压有无关系,并解释所的结论的在什么范围内有效。
| 有高血压 |
无高血压 |
合计 |
|
| 有吸烟史 |
81 |
2319 |
2400 |
| 无吸烟史 |
26 |
2074 |
2100 |
| 合计 |
107 |
4393 |
4500 |
对任意函数f(x),构造一个数列发生器。工作原理如下:
(1)输入数据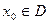 ,经数列发生器,输出
,经数列发生器,输出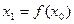 ;
;
(2)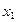 不属于D,则数列发生器结束工作;若
不属于D,则数列发生器结束工作;若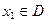 ,则数列发生器将x1反馈回输入端,再输出
,则数列发生器将x1反馈回输入端,再输出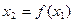 ,依次规律继续下去。画出发生器的流程图。
,依次规律继续下去。画出发生器的流程图。
.图1-1-17是一个几何体的三视图,试根据三视图说出这个几何体的名称,并画出这个几何体的直观图.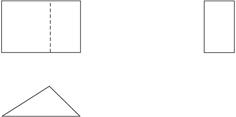
图1-1-17
画出图1-1-16中几何体的三视图.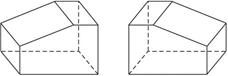
图1-1-16
已知圆柱的底面半径为r=10,高h=20,一只蚂蚁自下底面的A点爬到上底面的B′点,且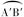 的长度是上底面圆周长的
的长度是上底面圆周长的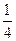 ,求由A爬到B的最短路程.
,求由A爬到B的最短路程.