某中学为丰富教工生活，国庆节举办教工趣味投篮比赛，有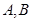
两个定点投篮位置，在
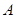点投中一球得2分，在
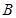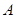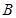点投中一球得3分。某规则是：按先后再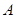的顺序投篮，教师甲在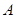和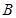点投中的概率分别是
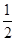和
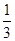，且在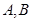两点投中与否相互独立。
（1）若教师甲投篮三次，试求他投篮得分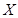
的分布列和数学期望；
（2）若教师乙与教师甲在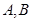投中的概率相同，两人按规则各投三次，求甲胜乙的概率。
设等差数列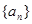
的前ｎ项的和为S n ,且S 4 =－62, S 6 =－75,求：
（1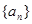）的通项公式a n及前ｎ项的和S n；
（2）|a 1 |+|a 2 |+|a 3 |+……+|a 14 |.
如图，为了测量河对岸A、B两点间的距离，在河的这边测得CD＝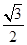
km，∠ADB＝∠CDB＝30°，∠ACD＝60°，∠ACB＝45°，求A、B两点间的距离．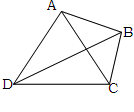
已知等差数列的首项为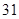
，若此数列从第
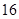项开始小于
，则公差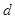
的取值范围
设集合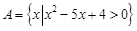
，
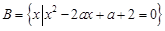，若
，求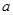
的取值范围.
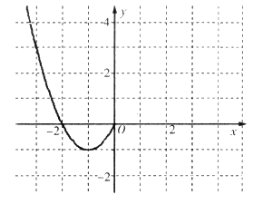
已知函数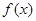
是定义在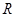
上的偶函数，且当
时，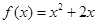
．现已画出函数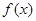在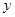
轴左侧的图象，如图所示，并根据图象：
（1）写出函数
的增区间；
（2）写出函数的解析式；
（3）若函数
，求函数
的最小值.