有编号为1,2,3的三个白球,编号为4,5,6的三个黑球,这六个球除编号和颜色外完全相同,现从中任意取出两个球.
(1)求取得的两个球颜色相同的概率;
(2)求取得的两个球颜色不相同的概率.
中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五名男记者和编号分别为6,7,8,9的四名女记者.要从这九名记者中一次随机选出两名,每名记者被选到的概率是相等的,用符号(x,y)表示事件“抽到的两名记者的编号分别为x、y,且x<y”.
(1)共有多少个基本事件?并列举出来;
(2)求所抽取的两名记者的编号之和小于17但不小于11或都是男记者的概率.
某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.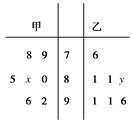
(1)求x和y的值;
(2)计算甲班七名学生成绩的方差.
设A,B分别是直线y=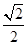 x和y=-
x和y=-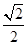 x上的动点,且|AB|=
x上的动点,且|AB|= ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足 =
=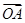 +
+ .
.
(1)求点P的轨迹方程;
(2)过点( ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
设点P是圆x2+y2=4上任意一点,由点P向x轴作垂线PP0,垂足为P0,且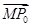 =
=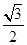
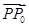 .
.
(1)求点M的轨迹C的方程;
(2)设直线l:y=kx+m(m≠0)与(1)中的轨迹C交于不同的两点A,B.
若直线OA,AB,OB的斜率成等比数列,求实数m的取值范围.