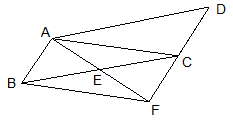
在如图的直角坐标系中，已知点A(2,0)、B(0，－4)，将线段AB绕点A按逆时针方向旋转90°至AC．
(1)求点C的坐标；
(2)若抛物线y＝－x2＋ax＋4经过点C．
①求抛物线的解析式；
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在，求出所有点P的坐标；若不存在，请说明理由．
请画出一条数轴，然后在所得的数轴上把下列各数表示出来：
3
，―4，―2，0，―1，1；并用“＜”连接.
把下列各数填在相应的大括号内：
15， 
， 0.81， -3， 
，－
， 0， 50％
负数集合{…}
正整数集合{…}
非负数集合{…}
有理数集合{…}
如图，△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝2，DC＝3，求AD的长.
小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题.请按照小萍的思路，探究并解答下列问题：
(1) 分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，求证：四边形AEGF是正方形；
(2) 设AD=x，建立关于x的方程模型，求出x的值.
某商店进了一批服装，进货单价为50元，如果按每件60元出售，可销售800件，如果每件提价1元出售，其销售量就减少20件．现在要获利12000元，且销售成本不超过24000元，问这种服装销售单价应定多少为宜？这时应进多少件服装？
如图，在平行四边形
中，
为
的中点，连接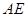
并延长交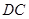
的延长线于点
．
(1)求证：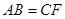
；
(2)当与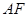
满足什么数量关系时，四边形
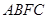是矩形，请说明理由．