甲乙丙丁4人玩传球游戏,持球者将球等可能的传给其他3人,若球首先从甲传出,经过3次传球.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为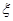 ,求
,求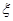 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知等差数列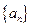 满足:
满足: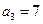 ,
,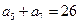 ,
,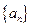 的前n项和为
的前n项和为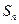 .
.
(Ⅰ)求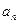 及
及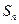 ;
;
(Ⅱ)令bn=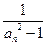 (
(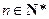 ),求数列
),求数列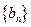 的前n项和
的前n项和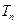 .
.
(本小题满分12分) 在△ABC中,已知B=45°,D是BC边上的一点,AD="10," AC=14,DC=6,求AB的长.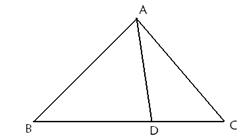
(本题满分12分)已知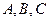 是直线
是直线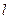 上三点,向量
上三点,向量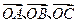 满足:
满足: ,且函数
,且函数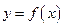 定义域内可导。
定义域内可导。
(1)求函数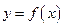 的解析式;
的解析式;
(2)若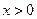 ,证明:
,证明: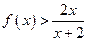 ;
;
(3)若不等式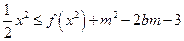 对
对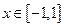 及
及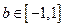 都恒成立,求实数
都恒成立,求实数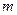 的取值范围。
的取值范围。
(本题满分12分)在平面直角坐标系中,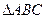 的两个顶点
的两个顶点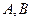 的坐标分别为
的坐标分别为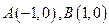 ,平面内两点
,平面内两点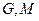 同时满足一下条件:①
同时满足一下条件:①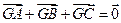 ;②
;②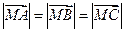 ;③
;③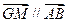
(1)求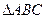 的顶点
的顶点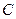 的轨迹方程;
的轨迹方程;
(2)过点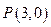 的直线
的直线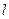 与(1)中的轨迹交于
与(1)中的轨迹交于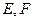 两点,求
两点,求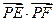 的取值范围。
的取值范围。
(本小题满分12分)已知数列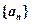 、
、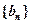 的前n项和分别为
的前n项和分别为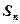 、
、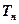 ,且满足
,且满足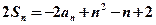 ,
,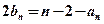 。
。
(Ⅰ)求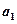 、
、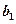 的值,并证明数列
的值,并证明数列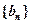 是等比数列;
是等比数列;
(Ⅱ)试确定实数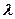 的值,使数列
的值,使数列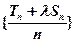 是等差数列。
是等差数列。