已知数列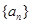 为等差数列,其公差d不为0,
为等差数列,其公差d不为0,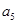 和
和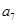 的等差中项为11,且
的等差中项为11,且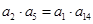 ,令
,令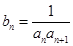 ,数列
,数列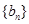 的前n项和为
的前n项和为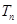 .
.
(1)求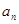 及
及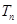 ;
;
(2)是否存在正整数m,n(1<m<n),使得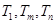 成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
(本小题满分14分)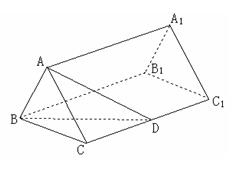
如图,已知正三棱柱 的底面边
的底面边 长是
长是 ,
, 是侧棱
是侧棱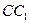 的中点,直线
的中点,直线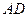 与侧面
与侧面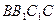 所成的角为
所成的角为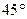 .
.
(1)求此正三棱柱的侧棱长;
(2)求二面角 的正切值;
的正切值;
(3)求点 到平面
到平面 的距离.
的距离.
(本小题满分12分)
某计算机程序每运行一次都随机出现一个二进制的六位 数
数 ,其中
,其中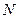 的各位数中,
的各位数中, ,
,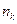 (
( 2,3,4,5)出现0的概率为
2,3,4,5)出现0的概率为 ,出现1的概率为
,出现1的概率为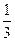 ,记
,记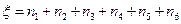
 ,当该计算机程序运行一次时,求随机变量
,当该计算机程序运行一次时,求随机变量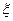 的分布列和数学期望(即均值).
的分布列和数学期望(即均值).
(本小题满分12分)
已知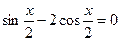 .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
(本小题满分14分)
已知函数 (
(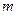 ,
,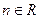 ,
, 且
且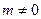 )的图象在
)的图象在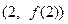 处的切线与
处的切线与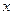 轴平行.
轴平行.
(I) 试确定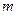 、
、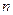 的符号;
的符号;
(II) 若函数 在区间
在区间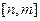 上有最大值为
上有最大值为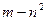 ,试求
,试求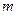 的值.
的值.
(本小题满分14分)
在数列 中,
中,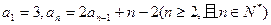
(1)求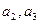 的值;
的值;
(2)证明:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(3)求数列 。
。