已知椭圆
经过点
，且两焦点与短轴的两个端点的连线构成一正方形.
（1）求椭圆
的方程；
（2）直线
与椭圆
交于
，
两点，若线段
的垂直平分线经过点
，求
（
为原点）面积的最大值.
（本小题满分14分）在钝角三角形ABC中，
、
、
分别是角A、B、C的对边，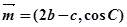
，
，且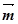
∥
.
（Ⅰ）求角A的大小；（Ⅱ）求函数
的值域．
（本题13分）
已知函数
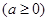（1）当
时，判断函数
在其定义域内是否存在极值？若存在，求出极值，若不存在，说明理由（2）若函数在其定义域内为单调函数，求
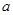的取值范围
（本题13分）
已知椭圆G：
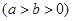的离心率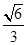为
，右焦点为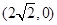
，斜率为1的直线
与椭圆G交于A,B两点，以AB为底的等腰三角形顶点为P（-3,2）
（1）求椭圆G的方程
（2）求
PAB的面积
（本题13分）数列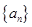
为等比数列，公比为
，
（1）求数列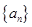的通项公式
（2）若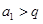
，求数列
的前
项和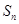
（本题12分）
在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥面ABCD, AP="AB," BP=BC=2，E,F分别是PB,PC的中点
（1）证明：EF
面PAD
（2）求三棱锥E-ABC的体积