在某中学举行的电脑知识竞赛中,将参赛学生的成绩(得分均为整数)进行整理后分成五组,绘制出频数分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
(1)求第二小组的频率,并补全这个频数分布直方图;
(2)求参赛的学生的优秀率(成绩≥80为优秀)和及格率(成绩≥60为及格);
(3)参赛学生成绩的中位数应落在第几小组内?(不必说明理由)
(4)请你评价一下这次竞赛的成绩.
如图，在平行四边形ABCD中, E为BC中点，AE的延长线与DC的延长线相交于点F.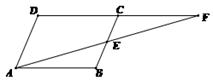
证明：∠DFA＝∠FAB；
证明：△ABE≌△FCE．
为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动. 对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）. 已知A、B两组捐款户数的比为1∶5.
请结合以上信息解答下列问题.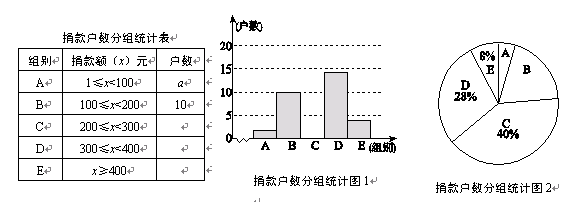
a=，本次调查样本的容量是；
先求出C组的户数，再补全“捐款户数分组统计图1”；
若该社区有500户住户，请根据以上信息估计，全社区捐款不少于300元的户数是多少？
解不等式组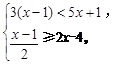
并求它的所有的非负整数解.
如图，在平面直角坐标系中，等腰直角三角形OMN的斜边ON在x轴上，顶点M的坐标为(3，3)，MH为斜边上的高．过N点垂直于x轴的直线与抛物线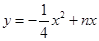
y=" -" 4x点D．直线OD的解析式为
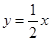，点P(x，o)是x轴上一动点，过点P作y轴的平行线，交射线OM与点E．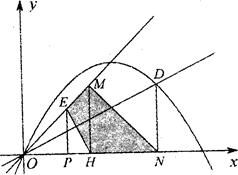
直接写出点D的坐标及n的值
判断抛物线的顶点是否在直线OM上？并说明理由
设以M、E、H、N为顶点的四边形的面积为S．当x≠3[时，求S与x的函数关系式．
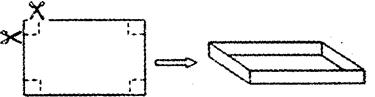
如图，把…张长10cm，宽8cm的矩形硬纸枥的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．要使长方体盒子的底面积为48cm2，那么剪去的正方形的边长为多少？
你感到折合而成的长方体盒子的侧面积（不含底面）会不会有最大的情况？如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由
