在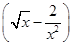 8的展开式中,
8的展开式中,
(1)系数的绝对值最大的项是第几项?
(2)求二项式系数最大的项;
(3)求系数最大的项;
(4)求系数最小的项.
本小题满分12分)
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<).
(1)求MN的长;
(2)当a为何值时,MN的长最小;
(3)当MN的长最小时,求面MNA与面MNB所成的二面角的余弦值.
(本小题满分12分)
在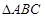 中,已知
中,已知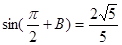 ,
,
(1) 求 的值;
的值;
(2) 若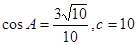 ,求
,求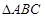 的面积;
的面积;
(3) 若函数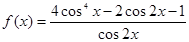 ,求
,求 的值.
的值.
(本小题满分14分)
已知函数 .
.
⑴若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
⑵若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数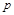 的取值范围;
的取值范围;
⑶设函数 ,若在
,若在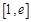 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数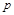 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆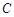 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线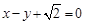 相切.
相切.
⑴求椭圆C的方程;
⑵设 ,
, 是椭圆
是椭圆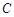 上的点,连结
上的点,连结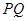 交椭圆
交椭圆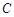 于另一点
于另一点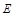 ,求直线
,求直线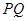 的斜率的取值范围.
的斜率的取值范围.
.(本小题满分13分)
在数列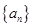 中,
中,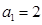 ,
,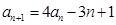 ,
,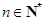 .
.
(1)证明数列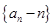 是等比数列;
是等比数列;
(2)设数列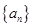 的前
的前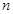 项和
项和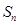 ,求
,求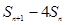 的最大值.
的最大值.